BYU PRISM

This nonlinear model library is a collection of process models consisting of differential and algebraic equations. Applications include processes from life sciences, energy research, electric vehicles, distillation, and benchmarking applications. The library spans traditional to cutting edge technologies. It serves as a valuable starting point for the development of more sophisticated control or estimation exercises or for specific applications.

CACHE News, 2008

Some models are developed in the MATLAB language while others are in the Gekko Optimization Suite (Python) or the APMonitor modeling language (Matlab and Python). The link in the Download column is a zipped archive of all files needed to simulate the system for MATLAB. For APMonitor or Gekko models it is a link to the source model page. Finally, the description gives a brief overview of the model. Similar models are generally grouped together with the simplest model appearing first.

Type	Download	Description
	Bioreactor	Zoltan K. Nagy's Dynamic simulator for a yeast fermentation bioreactor
	Blood Glucose	Blood Glucose Model for Type-I Diabetic
	Blood Glucose	Blood Glucose Model for Insulin Control
	Cell Culture	Cell culture population dynamics
	DC Motor	Electric Vehicle with Roger Aarenstrup's DC motor model
	Diet	Minimize cost while meeting nutritional needs
	Distillation 1	Distillation Column (Constant Relative Volatility)
	Distillation 1	Distillation Column (Constant Relative Volatility)
	Distillation 2	Distillation Column with Wilson Eq and Psat/P constant
	Distillation 3	Distillation Column with Wilson Equation
	Distillation 4	Distillation Column with Enthalpy Equation
	Electric Auto	Electric Vehicle
	Fermentation	Yang Zhang's yeast fermentation bioreactor model
	Fuel Cell	Ben Spivey's Solid Oxide Fuel Cell Model
	Fuel Ethanol	Industrial scale corn ethanol plant
	Gas Blend	Gas blending optimization problem
	Heated Rod	Heated Rod with Nonlinear Model Reduction by Proper Orthogonal Decomposition
	Hock Schittkowski	Test suite of 119 optimization problems
	Kite	Moritz Diehl's Dual String Kite Model
	Linear MPC	Model Predictive Control with Linear State Space Models
	Motor	DC Motor
	Oscillator	Electrical Oscillator
	Pendulum	Inverted Pendulum
	Pendulum	Inverted Pendulum
	Poly Reactor	Yang Zhang's polyethylene reactor model
	Reactor 1	CSTR with Jacket Dynamics (A->B)
	Reactor 1	CSTR with Jacket Dynamics (A->B)
	Reactor 2	CSTR with Jacket Dynamics (A-B-C-D)
	Reactor 3	CSTR with Jacket Dynamics (A->B->C)
	Reactor 4	2 CSTRs in Series (A->B)
	Reactor 5	2 CSTRs in Series with Jacket Dyn (A->B)
	Reactor 6	CSTR
	Shuttle	Endeavor Space Shuttle Launch
	Solar	Solar Collector
	Speed Control	Cruise Control
	Speed Control	Cruise Control (with Disturbance)
	Spring	Spring
	Stocks	Dow Jones Industrial Stocks
	Submarine	Underwater Vehicle
	Tank	Gravity Drained Water Tank
	Tank	Gravity Drained Water Tank
	TCLab PID	Temperature Control Lab (TCLab) Benchmark
	TCLab MPC	Advanced Modeling and Control Benchmark
	Thermo	Thermodynamic property data as a web service
	Yacht	Yacht engine control with approach to dock

The library consists of nonlinear models that include chemical reactors, binary distillation columns, and simple mechanical systems. The complexity of the models range from a simple ODE model with 1 input and 1 state to a large DAE model with 2 inputs and 125 states.

Presentation

Most of the models are taken from published articles. Currently, all the models are written in MATLAB, APMonitor, or Gekko. Each one has a step response driver where the model response is computed with an numerical solution engine such as the MATLAB integrator (e.g. ODE15s).

CSTR - Continuously Stirred Tank Reactor

The CSTR model with A->B exothermic reaction is the most popular model in the library. It is a standard model that has been used in reaction engineering textbooks, simulation and control research, and demonstrations for industrial software.

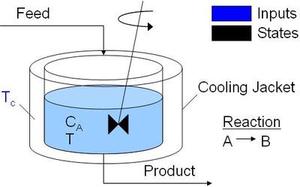
The model has 2 states: the concentration of A and the temperature of the reaction vessel liquid. The manipulated variable is the jacket water temperature. At a jacket temperature of 305K, the reactor model has an oscillatory response. The oscillations are characterized by reaction run-away with a temperature spike. When the concentration drops to a low value, the reactor cools until the concentration builds and there is another run-away reaction.

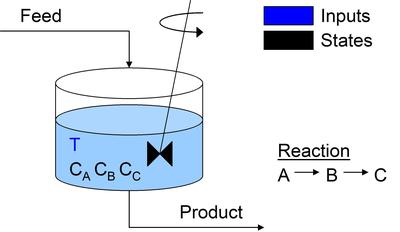
CSTR - Continuously Stirred Tank Reactor with Intermediate Species

Models 1-5, 10 are all variations of the CSTR model. Model 3 in particular, has a reaction intermediary (B). There is an additional equation and variable to account for the intermediate reaction step.

Binary Distillation Column with 30 trays (cyclohexane n-heptane)

Distillation column models are generally good test models for nonlinear model reduction and identification. The concentrations at each stage or tray are highly correlated. The dynamics of the distillation process can be described by a relatively few number of underlying dynamic states. A couple papers have been published with this model as an example application. One in particular is:

Hahn, J. and T.F. Edgar, An improved method for nonlinear model reduction using balancing of empirical gramians, Computers and Chemical Engineering, 26, pp. 1379-1397, (2002)

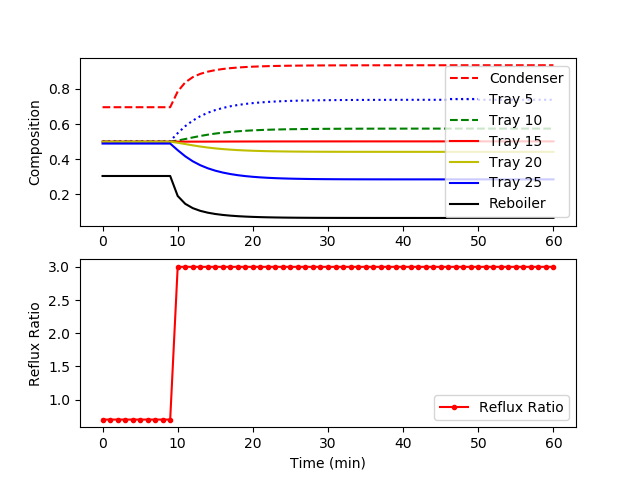
This response shows the system response after a step change in the reflux ratio. Each trajectory represents the mole fraction of cyclohexane at each tray. The top reflux material becomes less pure (more n-heptane) due to the increased draw from the top of the column.

Cruise Control with Disturbance

This simple mechanical model is of an object that is seeking to maintain constant speed while subject to disturbances. In this case, the disturbance is the incline or decline angle.

Gravity Drained Water Tank

This gravity drained water tank was a control experiment for Tom Edgar's undergraduate control course. The students had to perform experiments to determine the process time constant and tune a PID controller. The model gave excellent predictions of level (or volume) and was used to demonstrate the advantage of model predictive control (MPC) over PID control for level control.

The response shows the inlet valve 80% open for 60 seconds. The volume reaches 1400 mL before the inlet value is shut and the tank drains.

Human Blood Glucose Model for Insulin Control - Type I Diabetes

This model is combined from two related papers:

S. M. Lynch and B. W. Bequette, Estimation based Model Predictive Control of Blood Glucose in Type I Diabetes: A Simulation Study, Proc. 27th IEEE Northeast Bioengineering Conference, IEEE, 2001.

and

S. M. Lynch and B. W. Bequette, Model Predictive Control of Blood Glucose in type I Diabetics using Subcutaneous Glucose Measurements, Proc. ACC, Anchorage, AK, 2002.

It is a simple 3 state model that effectively describes blood glucose and insulin dynamics. The 3 states are plasma glucose concentration (mmol/L), plasma insulin concentration (mU/L) in remote compartment, and plasma insulin concentration (mU/L). The principal disturbance variable is the glucose input.

Yeast Fermentation Bioreactor

Zoltan Nagy contributed this model of a continuous plug flow fermentation reactor. Oxygen solubility is a function of the minerals that are present in solution.

You can make this library better by submitting your own models or improvements to the current set. Thousands of visitors download these models every month, making this site a great platform for disseminating research and networking with interested companies. For new submissions, please use the MathWorks File Exchange or post the model on Stack Overflow.