In Situ Adaptive Tabulation (ISAT)

ISAT is a nonlinear empirical modeling approach that adaptively builds models as new information is requested. ISAT has been applied to simulations of turbulent reacting flows as well as nonlinear model predictive control (NMPC) to make real-time applications feasible.  Like artificial neural networks, ISAT is a storage and retrieval method.  Unlike neural nets, ISAT is adaptive to extrapolation.  In addition, ISAT learns as it goes so there is no specified amount of training data before it starts performing.

ISAT approximates nonlinear function of dependent variables, y, as a function of independent variables, x. This is accomplished by dynamically constructing local linear approximations that are stored in a lookup database. 

Download Source Code

Animated Example

The animated graphic is an example with 2 independent variables (x and y as horizontal axes) and the 1 dependent variable (z as the vertical axis). ISAT approximates the function with multiple local linear regions. As the error tolerance increases, the approximation becomes increasingly granular to the point that individual linear regions can be observed.

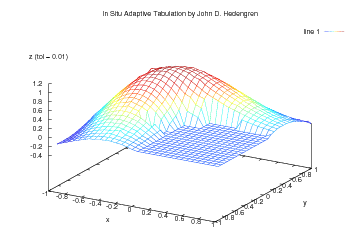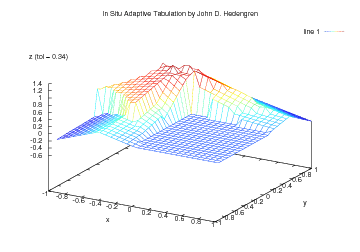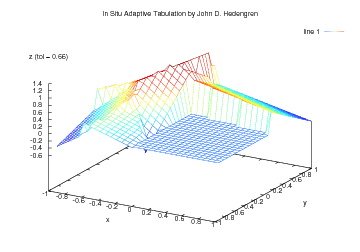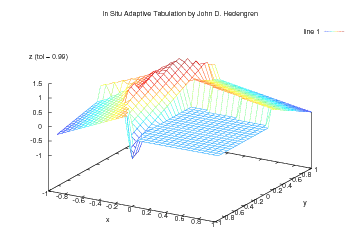
The animation shows an ISAT approximation to the first eigenfunction of an L-shaped membrane. The error tolerance for z is steadily ramped from 0.01 to 0.99. The error tolerance of the current frame is indicated on the figure. Initially at a low error tolerance of 0.01, the approximation is nearly exact but requires 206 ISAT records. When the error tolerance is increased to 0.1, 48 ISAT records are stored. At an error tolerance of 0.5, only 12 ISAT records are required to meet the relaxed error bound.    Explicit error control of the approximation of y is maintained by defining a region where the linear approximation is considered accurate. For n=1, this is a range on the value of x. For n=2, the estimate of the region of accuracy is an ellipse. For higher dimensional n, the estimate of the region of accuracy is a hyper-ellipsoid. For very nonlinear functions many linear approximations are required. For linear functions one record is required.    ISAT takes a fundamentally different approach to nonlinear function approximation. Most other function approximation approaches attempt to fit the entire nonlinear surface with one functional form. By using multiple local approximations, the functional form adapts to the nonlinear function. With this free functional form, ISAT is ideally suited for nonlinear functions with discontinuities or non-continuously differentiable points.   

Scenario 1: Retrieval

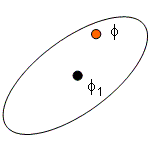
Scenario 2: Growth

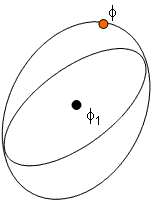
Scenario 3: Addition

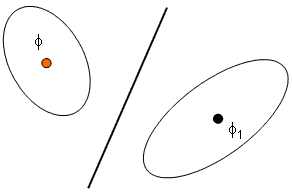
ISAT is suited to large-scale problems with O(n2+np) scaling, can approximate functions with discontinuities, explicitly limits approximation error, limits function approximation derivatives, and is adaptive to new data training without re-optimization. 

References

  1. Pope, S. B., "Computationally Efficient Implementation of Combustion Chemistry Using In Situ Adaptive Tabulation", Combustion Theory Modelling, 1997, 1, pp. 41-63.
  2. Hedengren, J. D. and Edgar, T. F., Approximate Nonlinear Model Predictive Control with In Situ Adaptive Tabulation, Computers and Chemical Engineering, Volume 32, pp. 706-714, 2008. Article
  3. Hedengren, J. D. and Edgar, T. F., In Situ Adaptive Tabulation for Real-Time Control, Industrial & Engineering Chemistry Research, Ind. Eng. Chem. Res., Volume 44, Issue 8, pp. 2716 -2724, 2005. Article
  4. Hedengren, J. D. and Edgar, T. F., In Situ Adaptive Tabulation for Real-time Control, Proceedings of the American Control Conference (ACC), Boston, MA, pp. 2222-2227, July 2004.